Can you explain?
Two persons are travelling in a car at the rate of 45 kmph and suddenly the person driving the car stops in front of a shop to buy some items and after purchasing the same, reaches the car when, to his surprise and dismay find the other person dead and moreover a stranger is inside the car. The stranger had not entered the car before they started nor the second person who was dead let him in while the first one went to the shop. What is the possible and logically correct explanation you can give?
Answer:
The two person were a man and his wife, and the lady was on labour and so they were rushing to a hospital enroute a shop to purchase some pills and the woman delivered a child and herself passed away in the post-delivery complications.
=================================================================================
Walk and ride: 2 pedestrians have one bike. They travel as follows: the first one rides the bike for some time, then drops it and continues walking in the same direction, while the second follows him by foot. Eventually, the second one finds the bike and rides it until he overtakes the first one. Then he gives the bike to the first one etc. Assuming that they walk with the same speed and bike faster than they walk, what is the speed of their travel?
Ans: The answer is: the harmonic average (the reciprocal of the arithmetic average of the reciprocals) of the walk and bike speeds. This is because both walk and bike equal distances.
===================================================================================
A few photos of Bobby Fischer

























































































a pictorial form of "Sieve of Erotosthenes"
The Euler product formula for the Riemann zeta function reads
where the left hand side equals the Riemann zeta function:
and the product on the right hand side extends over all prime numbers p:
[edit] Proof of the Euler product formula
This sketch of a proof only makes use of simple algebra that most high school students can understand. This was originally the method by which Euler discovered the formula. There is a certain sieving property that we can use to our advantage:
Subtracting the second from the first we remove all elements that have a factor of 2:
Repeating for the next term:
Subtracting again we get:
where all elements having a factor of 3 or 2 (or both) are removed.
It can be seen that the right side is being sieved. Repeating infinitely we get:
Dividing both sides by everything but the ζ(s) we obtain:
This can be written more concisely as an infinite product over all primes p:
| ζ(s) = | ∏ | (1 − p − s) − 1. |
| p |
To make this proof rigorous, we need only observe that when Re(s) > 1, the sieved right-hand side approaches 1, which follows immediately from the convergence of the Dirichlet series for ζ(s).
An interesting result can be found for ζ(1)
which can also be written as,
which is,
as, 
thus,
An elegant way to prove Square root of 2 is irrational.
If √2 were rational, we could write it as a fraction a/b in lowest terms. Then
a2=2b2.(Please read a squared = 2 x b squared
Look at the last digit of a2. It has to be 0, 1, 4, 5, 6 or 9. Now look at the last digit of 2b2. It has to be 0, 2 or 8. As a2 and 2b2 are the same number, its last digit must be 0. But that's only possible if a ends in 0 and b ends in 0 or 5. Either way both a and b are multiples of 5 contradicting a/b being in lowest terms.
==================================================================================



======================================================================
 Stare at the dot and slowly move your head towards the centre. What happens? Mystifying?
Stare at the dot and slowly move your head towards the centre. What happens? Mystifying?==================================================================================
 Follow the movement of the rotating pink dot with your eyes and the dots will remain only one color, pink. But if you stare at the black + in the center, the moving dot will turn green.
Follow the movement of the rotating pink dot with your eyes and the dots will remain only one color, pink. But if you stare at the black + in the center, the moving dot will turn green.================================================================================
 If you stare at one yellow dot for a while, the other yellow dots disappear.
If you stare at one yellow dot for a while, the other yellow dots disappear.=============================================================================
 From the picture cut out the six dismembered portions and try to set up to bring a complete normal horse.
From the picture cut out the six dismembered portions and try to set up to bring a complete normal horse.The Answer

===================================================================================
Watch tcworks2's Free Webcam
Watch ainuralm's Free Webcam
Watch pangaea2's Free Webcam


For those who are interested in seeing Nava Brindavana photos:
click here


In the following diagram of matchsticks denoting 4 cubes, remove just one matchstick to make it 3.

Answer: remove the back of the middle cube in the second row
Solution



Answer

In the following diagram, how many times the area of the bigger square when compared to the smallest square?

Answer

How will you take the Tennis ball out of trench shown in the following diagram?

Answer



Answer

Picturial proof for area of the inside triangle


Age puzzle


Answer:They are of the same age Proof:

Age of mom and dad


 This happened when the mother was 1 year old
This happened when the mother was 1 year oldnow the mother's age is 43
free stock charts from in.advfn.com

==================================================================================
Watch hetij's Free Webcam
Watch eugeap's Free Webcam
=======================================================================================







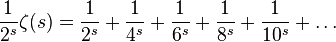
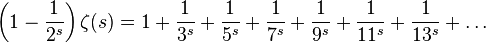






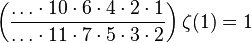


<< Home